Let's implement zlib.decompress()
Ever wondered how lossless compression in PNG files, ZIP files is achieved? In this article, we will attempt to gain some insight into it by writing a decompressor for the zlib format, which PNG and ZIP files use for compression!
Bit Reader
The zlib/DEFLATE spec is interesting in that it usually deals with streams of bits rather than bytes.
To make it easier to implement later algorithms, we shall first implement a BitReader class
which will handle the details of extracting individual bits and bytes from a bytestring:
class BitReader:
def __init__(self, mem):
self.mem = mem
self.pos = 0
self.b = 0
self.numbits = 0
def read_byte(self):
self.numbits = 0 # discard unread bits
b = self.mem[self.pos]
self.pos += 1
return b
def read_bit(self):
if self.numbits <= 0:
self.b = self.read_byte()
self.numbits = 8
self.numbits -= 1
# shift bit out of byte
bit = self.b & 1
self.b >>= 1
return bit
def read_bits(self, n):
o = 0
for i in range(n):
o |= self.read_bit() << i
return o
def read_bytes(self, n):
# read bytes as an integer in little-endian
o = 0
for i in range(n):
o |= self.read_byte() << (8 * i)
return oFor the DEFLATE spec, the rules of extracting bits from bytestring are as follows:
Given a byte, the first bit from DEFLATE's perspective (0th bit) is the byte's least significant bit, while the last bit from DEFLATE's perspective (7th bit) is the byte's most significant bit. e.g. for the byte
0x9d, the bits in from first to last are 1, 0, 1, 1, 1, 0, 0, 1.This is implemented in
read_bit(), which does this by first reading a byte (withread_byte()), shifting a bit out and then returning it. This continues for each call toread_bit()until all 8 bits have been shifted out, at which point it will read the next byte. Let's try it out:r = BitReader(b'\x9d') print(r.read_bit()) # 1 print(r.read_bit()) # 0 print(r.read_bit()) # 1 print(r.read_bit()) # 1 print(r.read_bit()) # 1 print(r.read_bit()) # 0 print(r.read_bit()) # 0 print(r.read_bit()) # 1 print(r.read_bit()) # IndexError: index out of rangeThe DEFLATE spec sometimes requires reading an unsigned integer
Icomprising ofnbits from the stream. In this case, the 1st bit that is read from the stream is the least significant bit, while then-th bit read from the stream is the most significant bit. For example, consider the integer299, which is0b100101011in binary (9 bits). Assuming that all the other bits are zero, this would be encoded as the two bytesb'\x2b\x01'.This is implemented in
read_bits(self, n), which implements this by callingread_bit()n times and placing the bit at the correct bit position. Let's try it out:r = BitReader(b'\x2b\x01') print(r.read_bits(9)) # 299The DEFLATE spec also sometimes requires reading an unsigned integer
Icomprising ofnbytes from the stream. In this case, whatever bits that were not read fromread_bits()/read_bit()are discarded, andnbytes are read. Thesenbytes are in little-endian order, that is, least significant byte first. For example, the integer13926is encoded asb'\x66\x36'.This is implemented in
read_bytes(self, n), which implements this by callingread_byte()n times and placing the bits of the bytes at the correct bit position. Let's try it out:r = BitReader(b'\x66\x36') print(r.read_bytes(2)) # 13926
The zlib container
Now that we have BitReader, let's start from the top.
The zlib format, starting from the start of the file/bytestring, is as follows:
- 1 byte:
CMF--- Compression Method and compression info fields - 1 byte:
FLG--- Compression flags fields - Variable number of bytes: The DEFLATE data
- 4 bytes:
ADLER32-- Adler-32 checksum over the original uncompressed data. For this exercise, we will simply ignore it. - End of file/bytestring
As we can see, the zlib format is a very lightweight container format over the DEFLATE format, adding only 6 extra bytes on top.
The CMF fields are as follows:
- Bits 0 to 3:
CM--- Compression Method. This identifies the compression method in the file. OnlyCM=8is defined by the zlib spec, which basically says that the zlib file contains data compressed with DEFLATE. Any other value ofCMis not supported, and we should error out. - Bits 4 to 7:
CINFO--- Compression info. This is the base-2 logarithm of the LZ77 window size, minus eight. In other words, the window size is . The maximum window size that is allowed by the spec is 32768, which is . In other words,CINFOmust be , and any other value should be treated as an error.
The FLG fields are as follows:
- Bits 0 to 4:
FCHECK--- Used as part of the checksum. See below. - Bits 5:
FDICT--- If set, aDICTdictionary identifier is present immediately after theFLGbyte. The dictionary is a sequence of bytes which is known beforehand to both the compressor and decompressor that can be used to achieve greater compression ratios. The zlib spec does not define any preset dictionaries and leaves it up to the implementor. The file formats that we are interested in (e.g. PNG, ZIP files) also do not specify any preset dictionaries. As such, we should not need to handle preset dictionaries at all, and we should error out if theFDICTbit is set. - Bits 6 to 7:
FLEVEL--- Compression level. This indicates whether the original data was compressed with the fastest/fast/default/max-compression compression level. It's not needed for de-compression at all, and is only there to indicate if recompression might be worthwhile. For our purposes, we can simply ignore it.
In addition, the CMF and FLG bytes also serve as a checksum: must be a multiple of 31.
Bits 0 to 4 in the FLG byte are set in the way that ensures that this is true if the CMF and FLG bytes are uncorrupted. This makes sense: since ,
and 5 bits can store values 0..31 inclusive, 5 bits is sufficient in ensuring that we can specify a value that is added to any integer to make it a multiple of 31.
As such, let's implement our top-level decompress() function:
def decompress(input):
r = BitReader(input)
CMF = r.read_byte()
CM = CMF & 15 # Compression method
if CM != 8: # only CM=8 is supported
raise Exception('invalid CM')
CINFO = (CMF >> 4) & 15 # Compression info
if CINFO > 7:
raise Exception('invalid CINFO')
FLG = r.read_byte()
if (CMF * 256 + FLG) % 31 != 0:
raise Exception('CMF+FLG checksum failed')
FDICT = (FLG >> 5) & 1 # preset dictionary?
if FDICT:
raise Exception('preset dictionary not supported')
out = inflate(r) # decompress DEFLATE data
ADLER32 = r.read_bytes(4) # Adler-32 checksum (for this exercise, we ignore it)
return outLet's say we have some zlib compressed data like this:
import zlib
x = zlib.compress(b'Hello World!')We should then be able to decompress it with our implemented decompress() function as follows:
print(decompress(x)) # Supposed to print b'Hello World!'Of course, it does not presently work because it calls inflate() to handle the DEFLATE data, but we haven't implemented inflate() yet.
We shall implement it in the following sections.
DEFLATE Blocks
A DEFLATE stream consists of a series of blocks. Each block begins with 3 header bits containing the following data:
| Bits | Name | Meaning |
|---|---|---|
| first bit | BFINAL | Set if and only if this is the last block of data. |
| next 2 bits | BTYPE | Specifies how the data are compressed, as follows:
|
As such, let's define the main function of our library, inflate(), which will inflate a compressed DEFLATE bitstream.
def inflate(r):
BFINAL = 0
out = [] # list of integers 0..255, representing decompressed bytes
while not BFINAL:
BFINAL = r.read_bit()
BTYPE = r.read_bits(2)
if BTYPE == 0:
inflate_block_no_compression(r, out)
elif BTYPE == 1:
inflate_block_fixed(r, out)
elif BTYPE == 2:
inflate_block_dynamic(r, out)
else:
raise Exception('invalid BTYPE')
return bytes(out) # return decompressed bytes as bytestringWe can't run it yet because it refers to missing functions inflate_block_no_compression(),
inflate_block_fixed() and inflate_block_dynamic() (you can stub them out for now).
In the rest of this article we will fill them up one by one.
Non-compressed blocks
Let's start out with something very simple -- non-compressed blocks. After the BFINAL and BTYPE bits, any bits of input up to the next byte boundary are ignored. Then, the rest of the block consists of:
- 2 bytes:
LEN--- the number of data bytes in the block. - 2 bytes:
NLEN-- the one's complement ofLEN. LENbytes: The literal data
As such, implementing inflate_block_no_compression() is trivial:
def inflate_block_no_compression(r, o):
LEN = r.read_bytes(2)
NLEN = r.read_bytes(2)
o.extend(r.read_byte() for _ in range(LEN))As mentioned when we were implementing BitReader,
read_bytes() will discard any unread bits and move to the next byte boundary,
which is what we want in this case.
At this point, our decompress() function will work for zlib bytestrings that have no compression! Let's try it out:
import zlib
x = zlib.compress(b'Hello World!', level=0) # level 0 means no compression
print(decompress(x)) # b'Hello World!'Now, let's move on to implement inflate_block_fixed() and inflate_block_dynamic()
so that we can handle compressed data.
To do that, we must first understand how DEFLATE does compression.
Huffman coding
The first half of DEFLATE's compression story is huffman coding. Here's an example to show how huffman coding works:
Suppose we only allow strings with the characters A, B, C and D.
Formally, this is called the alphabet .
An example of valid string which meets our conditions is "BBBACD".
An example of an invalid string is "BBBACDF",
since it contains the letter "F" which is not in our alphabet.
Now, let's say we want to encode the string "BBBACD" into binary.
One simple way to do it would be to map the characters of the alphabet to integers.
Since there are 4 characters in the alphabet, we will map them to the range 0..3 inclusive.
The maximum integer is 3, which requires at least 2 bits (b11 in binary) to represent,
and so we encode these integers with 2 bits each.
We map to 0 (binary: 0b00), to 1 (binary: 0b01), to 2 (binary: 0b10)
and to 3 (binary: 0b11).
The string "BBBACD" encoded in our simple encoding is thus 0b010101001011,
which is bits in total.
How could we compress the string "BBBACD" by encoding it with less bits?
Once way is to use a variable-length encoding which gives
shorter codes to more frequent characters.
A huffman code is a variable-length code table for encoding symbols of an alphabet into a string of bits. An example huffman code table for encoding the alphabet is:
| Symbol | Codeword |
|---|---|
A | 0b01 |
B | 0b1 |
C | 0b000 |
D | 0b001 |
One important constraint of a huffman code is that no codeword can be a prefix of another codeword.
For example, we can't assign B the codeword 0b0 because 0b0 is a prefix of A's codeword (0b01).
Likewise, we can't assign C the codeword 0b100 because B's codeword, 0b1, is a prefix of 0b100.
This constraint is needed to prevent ambiguity during decoding.
Let's say B is the codeword 0b0.
In that case, an ambiguity exists when decoding 0b001 --- should we decode it to "BA" or to "D"?
Now, we can see from the table that B can be encoded with 1 bit, A with 2 bits, and C and D
with 3 bits.
As such, the string "BBBACD" will be encoded as
0b11101000001,
which is 11 bits in total.
This is shorter than the simple encoding that we used earlier, and so compression has been achieved.
How would we encode 0b11101000001 into bytes?
The DEFLATE spec specifies that huffman-coded bits should be encoded in such a way that when reading it back
with BitReader, the first bit that read_bit() returns is the most significant bit (0b1),
the next bit that read_bit() returns is the second-most significant bit (0b1) etc.
To help us out later, let's implement code_to_bytes(code, n) which will help us do just that:
def code_to_bytes(code, n):
# Encodes a code that is `n` bits long into bytes that is conformant with DEFLATE spec
out = [0]
numbits = 0
for i in range(n-1, -1, -1):
if numbits >= 8:
out.append(0)
numbits = 0
out[-1] |= (1 if code & (1 << i) else 0) << numbits
numbits += 1
return bytes(out)Testing it out:
r = BitReader(code_to_bytes(0b11101000001, 11))
print([r.read_bit() for _ in range(11)]) # [1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1]Next, given a huffman code table like above, how could we write a program that can decode any arbitrary valid bitstream? One way would be to first convert the above table into a huffman tree. A huffman tree is a binary tree whose leaves are the symbols of the alphabet. For a given internal node, the left edge represents the bit 0 while the right edge represents the bit 1. The equivalent huffman tree for the huffman code in the table above is as follows:
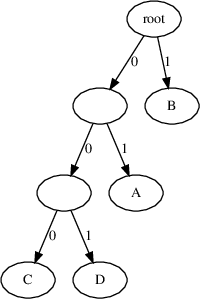
From the huffman tree, we can derive the codeword of a symbol by starting from the root and walking down
the edges to the leaf corresponding to the leaf, while noting down whether we took the left or right edge.
For example, to get to D from the root node, we first start from the root node, take the left edge (0),
then the left edge (0), then finally the right edge (1) to get to D,
which gives us the code 0b001 which is D's codeword in the table above!
Likewise, to decode a symbol from a bitstream, we can:
- Start from the root node.
- Read a bit from the bitstream. If it is a
0, take the left edge, otherwise (if it is a1), take the right edge. - Repeat Step 2 until we reach a leaf node. That is the decoded symbol.
As we can see, having a huffman tree makes it easy to write an algorithm that can decode symbols from a bitstream in linear time.
Now let's implement this. We start we the implementation of a HuffmanTree
that has an insert() operation that allows us to insert codeword -> symbol mappings into the tree
(with the assumption that they obey the "no codeword can be a prefix of another codeword" constraint).
class Node:
def __init__(self):
self.symbol = ''
self.left = None
self.right = None
class HuffmanTree:
def __init__(self):
self.root = Node()
def insert(self, codeword, n, symbol):
# Insert an entry into the tree mapping `codeword` of len `n` to `symbol`
node = self.root
for i in range(n-1, -1, -1):
b = codeword & (1 << i)
if b:
next_node = node.right
if next_node is None:
node.right = Node()
next_node = node.right
else:
next_node = node.left
if next_node is None:
node.left = Node()
next_node = node.left
node = next_node
node.symbol = symbolWe can now construct our example huffman tree as follows:
t = HuffmanTree()
t.insert(0b01, 2, 'A')
t.insert(0b1, 1, 'B')
t.insert(0b000, 3, 'C')
t.insert(0b001, 3, 'D')Then, we can write a decode_symbol() function that decodes a symbol from a bitstream using a specified huffman tree.
This is implemented using the algorithm described above:
def decode_symbol(r, t):
"Decodes one symbol from bitstream `r` using HuffmanTree `t`"
node = t.root
while node.left or node.right:
b = r.read_bit()
node = node.right if b else node.left
return node.symbolNow, let's try decoding 0b11101000001 back into "BBBACD":
r = BitReader(code_to_bytes(0b11101000001, 11))
print(decode_symbol(r, t)) # 'B'
print(decode_symbol(r, t)) # 'B'
print(decode_symbol(r, t)) # 'B'
print(decode_symbol(r, t)) # 'A'
print(decode_symbol(r, t)) # 'C'
print(decode_symbol(r, t)) # 'D'LZ77 and the Literal/Length and Distance Alphabet
One might imagine that the DEFLATE spec simply uses Huffman Coding as-is, but with an alphabet that consists of the values 0..255 inclusive, which are the values that a byte can take. That way, bytes which occur frequently in a file will be given shorter codewords, thus compressing the file. This is only half-correct --- the DEFLATE spec has an additional trick up its sleeve which achieve better compression ratios on files that contain repeated data: LZ77 compression.
Suppose we have a file that consists of the pattern "BBA" repeated over and over again, i.e. "BBABBABBABBA...".
Even if we encode B and A one bit each, the size of the compressed file will still be linear to the size of the
original file.
We can compress this file even further by employing LZ77 compression.
With LZ77 compression, we can first writing the literal values "BBA" into the output compressed file.
Next, rather than writing "BBA" again, we write a <length, backward distance> marker that specifies
that the (de-compressed) string of the specified length, backward distance away, should be duplicated.
For example, the string "BBABBA" (length 6) can be encoded as "BBA <3,3>",
the string "BBABBABBA" (length 9) can be encoded as "BBA <6,3>",
and the string "BBABBABBABBABBABBA" (length 18) can be encoded as "BBA <15,3>"!
This means that we can save nearly an exponential amount of space!
Now, using LZ77 compression as well means that a DEFLATE stream would contain both literal byte values and <length, backward distance> pairs. So, how does DEFLATE encode them and distinguish between them at de-compression time? It does this by defining two alphabets --- the Literal/Length alphabet and the Distance alphabet:
- The Literal/Length alphabet consists of the values 0..285 inclusive. Values 0..255 are the corresponding literal byte values. Value 256 is the end-of-block marker. Values 257..285 are used to encode the "length" portion of <length, backward distance> pairs, although it does not encode the length literally. See below.
- The Distance alphabet consists of the values 0..29 inclusive. They are used to encode the "backward distance" portion of <length, backward distance> pairs, although they do not encode them literally. See below.
These two alphabets each have their own huffman trees, which we shall call the Literal/Length tree and the Distance tree.
Values 257..285 of the Literal/Length alphabet are used to represent length values, sometimes in conjunction with extra bits that come after the symbol:
| Symbol | Extra bits | Length(s) |
|---|---|---|
| 257 | 0 | 3 |
| 258 | 0 | 4 |
| 259 | 0 | 5 |
| 260 | 0 | 6 |
| 261 | 0 | 7 |
| 262 | 0 | 8 |
| 263 | 0 | 9 |
| 264 | 0 | 10 |
| 265 | 1 | 11,12 |
| 266 | 1 | 13,14 |
| 267 | 1 | 15,16 |
| 268 | 1 | 17,18 |
| 269 | 2 | 19-22 |
| 270 | 2 | 23-26 |
| 271 | 2 | 27-30 |
| 272 | 2 | 31-34 |
| 273 | 3 | 35-42 |
| 274 | 3 | 43-50 |
| 275 | 3 | 51-58 |
| 276 | 3 | 59-66 |
| 277 | 4 | 67-82 |
| 278 | 4 | 83-98 |
| 279 | 4 | 99-114 |
| 280 | 4 | 115-130 |
| 281 | 5 | 131-162 |
| 282 | 5 | 163-194 |
| 283 | 5 | 195-226 |
| 284 | 5 | 227-257 |
| 285 | 0 | 258 |
Example 1: Let's say we call decode_symbol() with the literal/length huffman tree
and it returns 42.
Since it is within the range 0..255, it is a literal byte
and so we should write byte 42 to the output stream.
Example 2: Let's say we call decode_symbol() with the literal/length huffman tree
and it returns 256.
Since 256 is the end-of-block marker, we should terminate parsing of the block.
Example 3(a): Let's say we call decode_symbol() with the literal/length huffman tree and
it returns 257.
According to the table, symbol 257 has 0 extra bits.
Therefore we know immediately that we have reached a <length, backward distance> pair with length 3.
We then expect the backward distance of the pair to follow and we should next call decode_symbol() with the distance tree
to decode the backward distance. (See Example 3(b) for continuation)
Example 4(a): Let's say we call decode_symbol() with the literal/length huffman tree and it returns 275.
According to the table, symbol 275 has 3 extra bits.
We thus call read_bits(3) to read those 3 extra bits.
Let's say that read_bits(3) returns 2.
Therefore, we know that we have reached a <length, backward distance> pair with length 51 + 2 = 53.
We then expect the backward distance of the pair to follow and we should next call decode_symbol() with the distance tree
to decode the backward distance. (See Example 4(b) for continuation)
Similarly to the literal/length alphabet, the distance alphabet is used to represent backward distance values, sometimes in conjunction with extra bits that come after the symbol:
| Symbol | Extra Bits | Distance(s) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 2 |
| 2 | 0 | 3 |
| 3 | 0 | 4 |
| 4 | 1 | 5,6 |
| 5 | 1 | 7,8 |
| 6 | 2 | 9-12 |
| 7 | 2 | 13-16 |
| 8 | 3 | 17-24 |
| 9 | 3 | 25-32 |
| 10 | 4 | 33-48 |
| 11 | 4 | 49-64 |
| 12 | 5 | 65-96 |
| 13 | 5 | 97-128 |
| 14 | 6 | 129-192 |
| 15 | 6 | 193-256 |
| 16 | 7 | 257-384 |
| 17 | 7 | 385-512 |
| 18 | 8 | 513-768 |
| 19 | 8 | 769-1024 |
| 20 | 9 | 1025-1536 |
| 21 | 9 | 1537-2048 |
| 22 | 10 | 2049-3072 |
| 23 | 10 | 3073-4096 |
| 24 | 11 | 4097-6144 |
| 25 | 11 | 6145-8192 |
| 26 | 12 | 8193-12288 |
| 27 | 12 | 12289-16384 |
| 28 | 13 | 16385-24576 |
| 29 | 13 | 24577-32768 |
Example 3(b): After decoding the length of the <length, backward distance> pair in Example 3(a) and getting a length of 3,
we then call decode_symbol() with the distance tree to decode the backward distance.
Let's say decode_symbol() returns 2.
According to the table, symbol 2 has 0 extra bits.
Therefore we know immediately that we have a backward distance of 3,
and so our <length, backward distance> pair is .
As such, we should then copy 3 bytes 3 bytes back from the current position in the output stream to the output stream.
Example 4(b):
After decoding the length of the <length, backward distance> pair in Example 4(a) and getting a length of 53,
we then call decode_symbol() with the distance tree to decode the backward distance.
Let's say decode_symbol() returns 12.
According to the table, symbol 12 has 5 extra bits.
We thus call read_bits(5) to read those extra bits.
Let's say read_bits(5) returns 30.
Therefore, the backward distance is 65 + 30 = 95.
As such, we should then copy 53 bytes 95 bytes back from the current position in the output stream to the output stream.
Now let's implement it.
Firstly, we have the tables:
LengthExtraBits = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 0]
LengthBase = [3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31, 35, 43, 51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258]
DistanceExtraBits = [0, 0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 11, 11, 12, 12, 13, 13]
DistanceBase = [1, 2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193, 257, 385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145, 8193, 12289, 16385, 24577]LengthExtraBits is the "Extra bits" column of the Literal/Length table,
and LengthBase is the corresponding base integer of the "Length(s)" column of the Literal/Length table.
Likewise, DistanceExtraBits is the "Extra bits" column of the Distance table,
and DistanceBase is the corresponding base integer of the "Distance(s)" column of the Distance table.
And next, we have the decode function:
def inflate_block_data(r, literal_length_tree, distance_tree, out):
while True:
sym = decode_symbol(r, literal_length_tree)
if sym <= 255: # Literal byte
out.append(sym)
elif sym == 256: # End of block
return
else: # <length, backward distance> pair
sym -= 257
length = r.read_bits(LengthExtraBits[sym]) + LengthBase[sym]
dist_sym = decode_symbol(r, distance_tree)
dist = r.read_bits(DistanceExtraBits[dist_sym]) + DistanceBase[dist_sym]
for _ in range(length):
out.append(out[-dist])Encoding the literal/length and distance huffman trees
So, given the literal/length and distance huffman trees,
we can de-compress (or inflate) a block of data using our newly-implemented inflate_block_data() function.
However, how are these trees even stored in the first place?
Once way would be to just store the codeword -> symbol mappings as-is.
However, the DEFLATE spec uses a different method which allows huffman trees to be stored
more compactly in the file by placing additional restrictions on them.
In particular, the DEFLATE spec requires the huffman trees to be canonical huffman trees.
To recap, a huffman code is required to be a prefix code -- no codeword can be a prefix of another codeword.
On top of that, canonical huffman codes adds the following additional requirements:
- The first symbol whose codeword has bit length 1 must have the codeword of
0b0. - All codes of a given bit length have lexicographically consecutive values, in the same order as the symbols they represent.
- Shorter codes lexicographically precede longer codes.
For example, near the beginning of this article we had this example huffman code defined over the alphabet :
| Symbol | Codeword |
|---|---|
A | 0b01 |
B | 0b1 |
C | 0b000 |
D | 0b001 |
This is not a valid canonical huffman code, and thus cannot be encoded in the DEFLATE file. This is because:
- The first symbol whose codeword has bit length 1,
B, does not have a codeword of0b0, violating rule 1. Bhas a shorter code compared toA, but it is lexicographically greater compared toA, violating rule 3.
The fixed huffman code that meets all the conditions of being a canonical huffman code is:
| Symbol | Codeword |
|---|---|
A | 0b10 |
B | 0b0 |
C | 0b110 |
D | 0b111 |
Why require the huffman code to be canonical?
This is because any canonical huffman code can be uniquely compactly represented by (1) a list of the symbols of its alphabet (in the alphabet's order),
and (2) the bit length of the codeword for each symbol of the alphabet.
Furthermore, if the alphabet is already known by the decoder, then the alphabet list is not required at all,
and only the bit length list (which we shall call bl) needs to be provided.
For example, let's try to derive the canonical huffman code in the table above with just its alphabet and its bit length list bl.
To start off, the corresponding alphabet and bit length list bl is:
alphabet = 'ABCD'
bl = [2, 1, 3, 3]We also compute MAX_BITS, which is the size of the longest codeword:
MAX_BITS = max(bl)To derive the huffman tree, we first compute the number of codes for each code length.
bl_count = [sum(1 for x in bl if x == y and y != 0) for y in range(MAX_BITS+1)]
print(bl_count) # [0, 1, 1, 2]Next, we compute next_code such that next_code[n] is the smallest codeword with code length n.
next_code = [0, 0]
for bits in range(2, MAX_BITS+1):
next_code.append((next_code[bits-1] + bl_count[bits-1]) << 1)
print(next_code) # [0, 0, 2, 6]Sanity check: next_code[1] is 0 (binary: 0b0) which is correct since B's codeword is 0b0.
next_code[2] is 2 (binary: 0b10) which is correct since A's codeword is 0b10.
next_code[3] is 6 (binary: 0b110) which is correct since C's codeword is 0b110.
So everything seems fine.
Finally, we can compute the code for each symbol of our alphabet, and enter it into our huffman tree, taking care to ignore symbols of our alphabet whose codeword has a bit length of 0 (meaning the symbol is not used in the compressed data):
t = HuffmanTree()
for c, bitlen in zip(alphabet, bl):
if bitlen != 0: # ignore if bit length is 0
t.insert(next_code[bitlen], bitlen, c)
next_code[bitlen] += 1Now, let's try decoding b00010110111, which is "BBBACD":
r = BitReader(code_to_bytes(0b00010110111, 11))
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # A
print(decode_symbol(r, t)) # C
print(decode_symbol(r, t)) # DSo everything seems correct!
What happens if the alphabet is as usual,
but C and D are not used at all?
In that case, the DEFLATE spec specifies that C and D should be specified
as having bit length zero. In other words,
alphabet = 'ABCD'
bl = [2, 1, 0, 0]Furthermore, the DEFLATE spec allows trailing zeroes in the bl list to be ommitted.
In other words, this is valid:
alphabet = 'ABCD'
bl = [2, 1]To wrap up, here is a reusable bl_list_to_tree() function which
constructs a huffman tree from a bit length list, implemented using all the algorithms we have covered in this section:
def bl_list_to_tree(bl, alphabet):
MAX_BITS = max(bl)
bl_count = [sum(1 for x in bl if x == y and y != 0) for y in range(MAX_BITS+1)]
next_code = [0, 0]
for bits in range(2, MAX_BITS+1):
next_code.append((next_code[bits-1] + bl_count[bits-1]) << 1)
t = HuffmanTree()
for c, bitlen in zip(alphabet, bl):
if bitlen != 0:
t.insert(next_code[bitlen], bitlen, c)
next_code[bitlen] += 1
return tUsage:
t = bl_list_to_tree([2, 1, 3, 3], 'ABCD')
r = BitReader(code_to_bytes(0b00010110111, 11))
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # B
print(decode_symbol(r, t)) # A
print(decode_symbol(r, t)) # C
print(decode_symbol(r, t)) # DHowever, the DEFLATE spec adds yet another twist. Rather than just specifying the code lengths directly, for "even greater compactness", the code length sequences themselves are compressed using a Huffman code! The alphabet for the code lengths is as follows:
| Symbol | Meaning |
|---|---|
| 0 - 15 | Represent code lengths of 0 - 15 |
| 16 | Copy the previous code length 3 - 6 times. The next 2 bits indicate repeat length ( 0 = 3, ..., 3 = 6) |
| 17 | Repeat a code length of 0 for 3 - 10 times. (3 bits of length) |
| 18 | Repeat a code length of 0 for 11 - 138 times. (7 bits of length) |
To make this clear: we actually now have three huffman codes in play here --- the code length huffman code, the literal/length huffman code and the distance huffman code. For clarity let's give them mathematical symbols as follows:
- Let be the code length alphabet (the table directly above).
- Let be the code length huffman tree.
- Let be the code length list of .
- Let be the literal/length huffman tree.
- Let be the code length list of .
- Let be the distance huffman tree.
- Let be the code length list of .
- Let be encoded using the code length alphabet and then compressed using the code length huffman tree .
The code length, literal/length and distance huffman trees are stored as bits in the DEFLATE file as follows:
- 5 bits:
HLIT, the number of literal/length codes () minus 257. In other words, . - 5 bits:
HDIST: the number of distance codes () minus 1. In other words, . - 4 bits:
HCLEN: the number of code length codes () minus 4. In other words, . - (
HCLEN+ 4) x 3 bits: code lengths for the code length alphabet given just above, in the order: 16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15. In other words, , but the elements are in a different order --- we will need to rearrange them back. - Variable number of bits follows, containing the code length list for the literal/length alphabet () followed by the code length list for the distance alphabet (), encoded using the code length alphabet and huffman code. In other words, .
To wrap everything up, let's implement a function decode_trees()
which will read the relevant bits from the input BitReader stream and decode them into
the literal/length and distance huffman trees:
CodeLengthCodesOrder = [16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15]
def decode_trees(r):
# The number of literal/length codes
HLIT = r.read_bits(5) + 257
# The number of distance codes
HDIST = r.read_bits(5) + 1
# The number of code length codes
HCLEN = r.read_bits(4) + 4
# Read code lengths for the code length alphabet
code_length_tree_bl = [0 for _ in range(19)]
for i in range(HCLEN):
code_length_tree_bl[CodeLengthCodesOrder[i]] = r.read_bits(3)
# Construct code length tree
code_length_tree = bl_list_to_tree(code_length_tree_bl, range(19))
# Read literal/length + distance code length list
bl = []
while len(bl) < HLIT + HDIST:
sym = decode_symbol(r, code_length_tree)
if 0 <= sym <= 15: # literal value
bl.append(sym)
elif sym == 16:
# copy the previous code length 3..6 times.
# the next 2 bits indicate repeat length ( 0 = 3, ..., 3 = 6 )
prev_code_length = bl[-1]
repeat_length = r.read_bits(2) + 3
bl.extend(prev_code_length for _ in range(repeat_length))
elif sym == 17:
# repeat code length 0 for 3..10 times. (3 bits of length)
repeat_length = r.read_bits(3) + 3
bl.extend(0 for _ in range(repeat_length))
elif sym == 18:
# repeat code length 0 for 11..138 times. (7 bits of length)
repeat_length = r.read_bits(7) + 11
bl.extend(0 for _ in range(repeat_length))
else:
raise Exception('invalid symbol')
# Construct trees
literal_length_tree = bl_list_to_tree(bl[:HLIT], range(286))
distance_tree = bl_list_to_tree(bl[HLIT:], range(30))
return literal_length_tree, distance_treePutting everything together: handling compressed blocks
We are now ready to write the implementations of inflate_block_dynamic() (decompress block compressed with dynamic huffman codes) and inflate_block_fixed() (decompress block with fixed huffman codes)!
With the decode_trees() and inflate_block_data() function we have painstakenly implemented over multiple sections,
it is now trivial to implement inflate_block_dynamic() ---
we simply first read in and decode the literal/length and distance huffman trees with decode_trees(),
and then call inflate_block_data() to inflate the compressed data that follows:
def inflate_block_dynamic(r, o):
# decompress block with dynamic huffman codes
literal_length_tree, distance_tree = decode_trees(r)
inflate_block_data(r, literal_length_tree, distance_tree, o)With inflate_block_fixed(), the literal/length and distance huffman codes are not specified in the compressed file, but rather is known to the decompressor beforehand.
The DEFLATE spec specifies the literal/length huffman code in terms of bitlengths, which we can then use to construct a canonical huffman tree with bl_list_to_tree() that we implemented earlier:
| Literal/length symbol | Bit length of codeword |
|---|---|
| 0 - 143 | 8 |
| 144 - 255 | 9 |
| 256 - 279 | 7 |
| 280 - 287 | 8 |
Eagle-eyed readers will notice that literal/length symbols 286-287 are mentioned in the table,
but are actually not part of the length/literal alphabet.
They will not occur in compressed data, but participate in the code construction in bl_list_to_tree(), particularly in the computation of bl_count.
Likewise, the DEFLATE spec specifies the distance huffman code in terms of bitlengths:
| Distance symbol | Bit length of codeword |
|---|---|
| 0 - 29 | 5 |
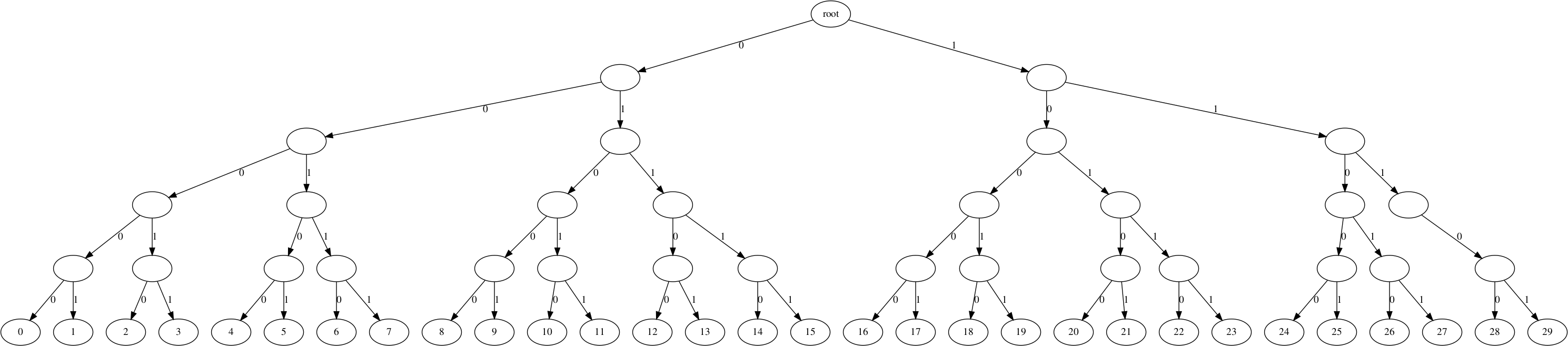
For reference, here is how the fixed literal/length huffman tree looks like:
And here is how the fixed distance huffman tree looks like:
We can implement inflate_block_fixed() as follows:
def inflate_block_fixed(r, o):
bl = ([8 for _ in range(144)] + [9 for _ in range(144, 256)] +
[7 for _ in range(256, 280)] + [8 for _ in range(280, 288)])
literal_length_tree = bl_list_to_tree(bl, range(286))
bl = [5 for _ in range(30)]
distance_tree = bl_list_to_tree(bl, range(30))
inflate_block_data(r, literal_length_tree, distance_tree, o)Full source code
And we are done! We can test out our newly-minted decompress() function with:
import zlib
x = zlib.compress(b'Hello World!')
print(decompress(x)) # b'Hello World!'Here is the full source code listing:
class BitReader:
def __init__(self, mem):
self.mem = mem
self.pos = 0
self.b = 0
self.numbits = 0
def read_byte(self):
self.numbits = 0 # discard unread bits
b = self.mem[self.pos]
self.pos += 1
return b
def read_bit(self):
if self.numbits <= 0:
self.b = self.read_byte()
self.numbits = 8
self.numbits -= 1
# shift bit out of byte
bit = self.b & 1
self.b >>= 1
return bit
def read_bits(self, n):
o = 0
for i in range(n):
o |= self.read_bit() << i
return o
def read_bytes(self, n):
# read bytes as an integer in little-endian
o = 0
for i in range(n):
o |= self.read_byte() << (8 * i)
return o
def decompress(input):
r = BitReader(input)
CMF = r.read_byte()
CM = CMF & 15 # Compression method
if CM != 8: # only CM=8 is supported
raise Exception('invalid CM')
CINFO = (CMF >> 4) & 15 # Compression info
if CINFO > 7:
raise Exception('invalid CINFO')
FLG = r.read_byte()
if (CMF * 256 + FLG) % 31 != 0:
raise Exception('CMF+FLG checksum failed')
FDICT = (FLG >> 5) & 1 # preset dictionary?
if FDICT:
raise Exception('preset dictionary not supported')
out = inflate(r) # decompress DEFLATE data
ADLER32 = r.read_bytes(4) # Adler-32 checksum (for this exercise, we ignore it)
return out
def inflate(r):
BFINAL = 0
out = []
while not BFINAL:
BFINAL = r.read_bit()
BTYPE = r.read_bits(2)
if BTYPE == 0:
inflate_block_no_compression(r, out)
elif BTYPE == 1:
inflate_block_fixed(r, out)
elif BTYPE == 2:
inflate_block_dynamic(r, out)
else:
raise Exception('invalid BTYPE')
return bytes(out)
def inflate_block_no_compression(r, o):
LEN = r.read_bytes(2)
NLEN = r.read_bytes(2)
o.extend(r.read_byte() for _ in range(LEN))
def code_to_bytes(code, n):
# Encodes a code that is `n` bits long into bytes that is conformant with DEFLATE spec
out = [0]
numbits = 0
for i in range(n-1, -1, -1):
if numbits >= 8:
out.append(0)
numbits = 0
out[-1] |= (1 if code & (1 << i) else 0) << numbits
numbits += 1
return bytes(out)
class Node:
def __init__(self):
self.symbol = ''
self.left = None
self.right = None
class HuffmanTree:
def __init__(self):
self.root = Node()
self.root.symbol = ''
def insert(self, codeword, n, symbol):
# Insert an entry into the tree mapping `codeword` of len `n` to `symbol`
node = self.root
for i in range(n-1, -1, -1):
b = codeword & (1 << i)
if b:
next_node = node.right
if next_node is None:
node.right = Node()
next_node = node.right
else:
next_node = node.left
if next_node is None:
node.left = Node()
next_node = node.left
node = next_node
node.symbol = symbol
def decode_symbol(r, t):
"Decodes one symbol from bitstream `r` using HuffmanTree `t`"
node = t.root
while node.left or node.right:
b = r.read_bit()
node = node.right if b else node.left
return node.symbol
LengthExtraBits = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
3, 4, 4, 4, 4, 5, 5, 5, 5, 0]
LengthBase = [3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31, 35, 43,
51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258]
DistanceExtraBits = [0, 0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7,
8, 8, 9, 9, 10, 10, 11, 11, 12, 12, 13, 13]
DistanceBase = [1, 2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193, 257,
385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145, 8193, 12289, 16385,
24577]
def inflate_block_data(r, literal_length_tree, distance_tree, out):
while True:
sym = decode_symbol(r, literal_length_tree)
if sym <= 255: # Literal byte
out.append(sym)
elif sym == 256: # End of block
return
else: # <length, backward distance> pair
sym -= 257
length = r.read_bits(LengthExtraBits[sym]) + LengthBase[sym]
dist_sym = decode_symbol(r, distance_tree)
dist = r.read_bits(DistanceExtraBits[dist_sym]) + DistanceBase[dist_sym]
for _ in range(length):
out.append(out[-dist])
def bl_list_to_tree(bl, alphabet):
MAX_BITS = max(bl)
bl_count = [sum(1 for x in bl if x == y and y != 0) for y in range(MAX_BITS+1)]
next_code = [0, 0]
for bits in range(2, MAX_BITS+1):
next_code.append((next_code[bits-1] + bl_count[bits-1]) << 1)
t = HuffmanTree()
for c, bitlen in zip(alphabet, bl):
if bitlen != 0:
t.insert(next_code[bitlen], bitlen, c)
next_code[bitlen] += 1
return t
CodeLengthCodesOrder = [16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15]
def decode_trees(r):
# The number of literal/length codes
HLIT = r.read_bits(5) + 257
# The number of distance codes
HDIST = r.read_bits(5) + 1
# The number of code length codes
HCLEN = r.read_bits(4) + 4
# Read code lengths for the code length alphabet
code_length_tree_bl = [0 for _ in range(19)]
for i in range(HCLEN):
code_length_tree_bl[CodeLengthCodesOrder[i]] = r.read_bits(3)
# Construct code length tree
code_length_tree = bl_list_to_tree(code_length_tree_bl, range(19))
# Read literal/length + distance code length list
bl = []
while len(bl) < HLIT + HDIST:
sym = decode_symbol(r, code_length_tree)
if 0 <= sym <= 15: # literal value
bl.append(sym)
elif sym == 16:
# copy the previous code length 3..6 times.
# the next 2 bits indicate repeat length ( 0 = 3, ..., 3 = 6 )
prev_code_length = bl[-1]
repeat_length = r.read_bits(2) + 3
bl.extend(prev_code_length for _ in range(repeat_length))
elif sym == 17:
# repeat code length 0 for 3..10 times. (3 bits of length)
repeat_length = r.read_bits(3) + 3
bl.extend(0 for _ in range(repeat_length))
elif sym == 18:
# repeat code length 0 for 11..138 times. (7 bits of length)
repeat_length = r.read_bits(7) + 11
bl.extend(0 for _ in range(repeat_length))
else:
raise Exception('invalid symbol')
# Construct trees
literal_length_tree = bl_list_to_tree(bl[:HLIT], range(286))
distance_tree = bl_list_to_tree(bl[HLIT:], range(30))
return literal_length_tree, distance_tree
def inflate_block_dynamic(r, o):
literal_length_tree, distance_tree = decode_trees(r)
inflate_block_data(r, literal_length_tree, distance_tree, o)
def inflate_block_fixed(r, o):
bl = ([8 for _ in range(144)] + [9 for _ in range(144, 256)] +
[7 for _ in range(256, 280)] + [8 for _ in range(280, 288)])
literal_length_tree = bl_list_to_tree(bl, range(286))
bl = [5 for _ in range(30)]
distance_tree = bl_list_to_tree(bl, range(30))
inflate_block_data(r, literal_length_tree, distance_tree, o)
import zlib
x = zlib.compress(b'Hello World!')
print(decompress(x)) # b'Hello World!'